Online Ableitungsrechner mit Rechenweg
Online Ableitungsrechner
Lösung
Wird bearbeitet...

Der Ableitungsrechner, den wir Ihnen hier zur Verfügung stellen, ist ein großartiges Werkzeug zur Lösung aller Arten von Derivaten und bietet detaillierte Schritt-für Schritt-Lösungen. Dies ist zweifellos der beste Rechner, der online abgeleitet werden kann. Zusätzlich zum ableitungsrechner erläutern wir auch alle grundlegenden Konzepte, die zum Erlernen der Ableitung von Funktionen erforderlich sind.
Anleitung zur Verwendung des Online AbleitungsRechner
Die Verwendung des Ableitungsrechners ist sehr einfach, geben Sie einfach die Funktion ein, die Sie ableiten wollen, und drücken dann die Schaltfläche „Berechnen„.
Nachfolgend finden sie die Befehle und Operatoren, die Sie mit diesem abgeleiteten Rechner verwenden müssen.
Dieser Ableitungsrechner arbeitet damitig mit Einzelvariablenfunktionen. Um den Ableitungsrechner verwenden zu können, müssen Sie die Funktionen mit der Variablen x eingeben.
Was ist Differentialrechnung?
Bei der Differentialrechnung wird untersucht, wie sich Funktionen ändern, wenn sich ihre Variablen ändern.
Was ist eine Ableitung?
Eine Ableitung gibt die Änderung des Funktionswertes an, d.h. die Steigung des Funktionsgraphen an einer bestimmten Stelle. Die Ableitung ist einer der grundpfeiler der mathematik.
Geometrische Interpretation der Ableitung
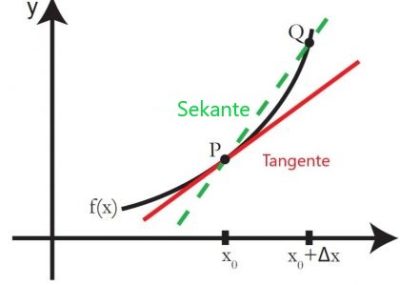
Die Ableitung von f(x) in x=x0 ist die Steigung der Tangente an den graphen f(x) in dem punkt P(f(x0),x0). Die tangentenlinie ist die grenze der sekantenlinie der punkte P(f(x0),x0) und Q auf dem diagramm von f(x) wenn Q wenn P nähert.
Wie auf dem bild zu sehen ist, berührt die tangente die kurve von f(x) in dem punkt P(f(x0),x0); die steigung der tangentenlinie fällt mit der richtung der kurve an diesem punkt. Die tangente ist die gerade, die die kurve am besten an den punkt P heranführt. Angesichts eines diagramms unserer funktion ist es für uns nicht schwer, die tangentenlinie grafisch darzustellen.Wir wollen jedoch berechnungen mit der tangentenlinie durchführen.Daher benötigen wir eine rechnerische methode, um die tangente zu finden.
Wir wissen, dass die gleichung einer geraden mit steigung m am punkt P(f(x0),x0) ist y−y0=m(x−x0), und diese Gleichung ist die abstrakte Form der Tangentengleichung. Wenn wir die spezifische Gleichung der Tangentengleichung finden wollen, dann müssen wir zuerst die Werte der Koordinate (f(x0),x0), und dafür müssen wir nur den wert von kennen x0 zu kennen und diesen in der Funktion zu ersetzen, die wir den Wert von f(x0). Zweitens müssen wir den Wert der Steigung kennen, m=f‚(f(x0)), den wir sterben Ableitung der Funktion nennen.
Mit all diesen Informationen können wir die folgende Definition festlegen:
Die Ableitung von f‚(x0) von f bei x0 ist die Steigung der Tangente der Kurvey=f(t) punkt P(f(x0),x0).
Wenn wir mit der geometrischen Interpretation der Ableitung fortfahren, wiseen wir, dass die Sekantenlinie eine Linie ist, die die Kurve der Funktion an zwei Punkten schneidet, wie man im vorherigen Bild sieht. Wenn der Trennungsabstand zwischen den Punkten klein genug istdann nähert sich der Wert der Steigung der Sekantenlinie dem Wert der Steigung der Kurve. Daher wenn wir die Steigung der Tangentenlinie mm finden wollen, die gleich dem Wert der Steigung der Kurve ist, können wir sie durch Annäherung finden, indem wir die Steigung der Sekantenlinie berechnen. Nehmen wir an, dass die PQ Linie die Sekantenlinie der Kurve f(x) ist.
Wir können die Steigung des Graphen in P finden, indem wir die Steigung von PQ berechnen als dass Q immer näher an P herankommt (und die Steigung vonPQ immer näher an m herankommt).
Die Linie Tangente gleich der Grenze der PQ Sekantenlinien ist, wie z.B. Q→P; wobei P fest bleibt und Q näher kommt.
Wir beginnen am P(x0,f(x0)), und bewegen uns dann eine kleine Strecke weiterhorizontal Δx und finden so den Punkt Q(x0+Δx,f(x0+Δx)).
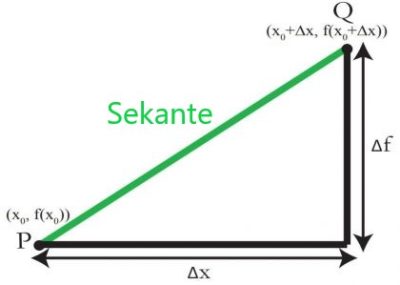
Diese beiden Punkte liegen auf einer Sekantenlinie des Graphen von f(x). Der vertikale Unterschied zwischen P und Q ist Δf=f(x0+Δx)–f(x0). Die Steigung des sekanten PQ ist durch das Verhältnis Δf/Δx gegeben. Zuvor haben wir festgestellt, dass die Tangentenlinie die Grenze der Sekantenlinie ist. Auch stimmt es , dass die Steigung der Tangentenlinie die Grenze der Steigungen der Sekantenlinie ist Mit anderen Worten:
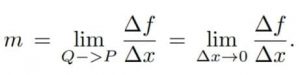
Von hier aus können wir feststellen, was die Ableitung einer gegebenen Funktion in x0 ist:
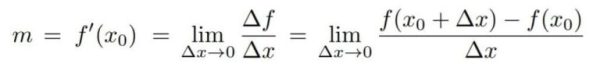
Wenn wir das wissen, haben wir die allgemeine Formel der Ableitung einer Funktion wie folgt:

Ableitungsregeln
Ableitung einer Konstanten

Faktorregel
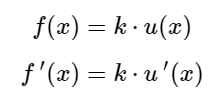
Potenzregel

Summenregel

Produktregel

Quotientenregel
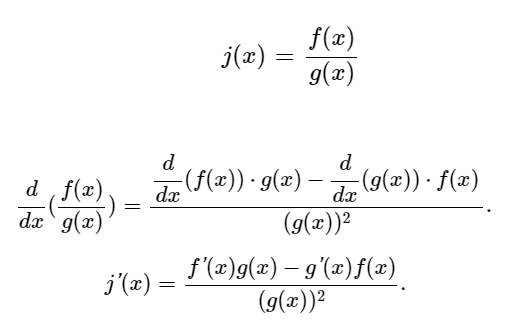
Kettenregel

Die Vorteile des Studiums mit einem Ableitungsrechner online
Mathematik ist eine der grundlegenden Wissenschaften und ein wichtiger Bestandteil unseres täglichen Lebens. Es hilft uns, Probleme zu lösen, logisch zu denken und Entscheidungen zu treffen. Trotz ihrer Bedeutung kann Mathematik jedoch für viele Menschen eine Herausforderung darstellen. Vor allem, wenn es um komplexe Berechnungen und Ableitungen geht.
Hier kommt ein Ableitungsrechner online ins Spiel. Eine solche Online-Tool bietet viele Vorteile für Schüler, Studierende und Mathematik-Enthusiasten. Es ist eine benutzerfreundliche und zuverlässige Lösung, um Ableitungen schnell und einfach zu berechnen. Einfach die Funktion eingeben und schon erhalten Sie das Ergebnis, ohne dass Sie sich mit manuellen Berechnungen oder komplizierten Formeln herumschlagen müssen.
Einer der größten Vorteile eines Ableitungsrechners online ist die Zeitersparnis. Schüler und Studierende müssen nicht länger Stunden damit verbringen, komplexe Ableitungen manuell zu berechnen, sondern können stattdessen ihre Zeit darauf verwenden, die Konzepte besser zu verstehen und zu üben. Außerdem kann ein Ableitungsrechner online Fehler in der Berechnung vermeiden und sicherstellen, dass die Antworten korrekt sind.
Ein weiterer Vorteil ist die Verfügbarkeit. Ein Ableitungsrechner online kann von überall auf der Welt genutzt werden, solange eine Internetverbindung besteht. Schüler und Studierende können ihn zu Hause, im Unterricht oder sogar unterwegs nutzen, was es einfacher macht, jederzeit und überall zu lernen.
Ein Ableitungsrechner online ist auch eine großartige Ressource für Lehrer. Sie können es nutzen, um Schülern bei den Berechnungen zu helfen, aber auch um sicherzustellen, dass die Antworten korrekt sind. Außerdem können Lehrer es nutzen, um Schülern praktische Übungen zu geben und das Verständnis für komplexe Konzepte zu verbessern.
Hergestellt mit ❤